Selamat datang di blog saya,
Pada kesempatan kali ini, kita akan berbagi pengalaman materi ajar pegas. Susunan seri atau pun susunan paralel pegas pada dasarnya memiliki tujuan tertentu. Misalnya susunan pegas yang disengaja disusun seri, bertujuan untuk memperkecil nilai konstanta pegas. Sehingga pertambahan yang dialami sistem pegas akan lebih besar. Sedangkan susunan paralel bertujuan untuk memperbesar nilai konstanta pegas. Sehingga pertambahan panjang sistem pegas lebih kecil.
Mata Pelajaran : Fisika
Kelas :
XI MIPA
Materi Ajar :
Pegas
Hari/tanggal :
……………………………………..
Waktu :
……………………………………..
Pada
susunan seri, pertambahan panjang sistem pegas sama dengan jumlah pertambahan
panjang masing – masing pegas. Sedangkan pada susunan paralel, masing – masing pegas
mengalami pertambahan panjang yang sama besar, yaitu sama dengan pertambahan
sistem pegasnya.
Contoh : 1
Tiga
buah pegas identik dengan konstanta elastisitas masing – masing 85 N/m disusun
paralel. Maka tentukan konstanta pengganti dari rangkaian pegas.
Pembahasan :
Diketahui,
Konstanta
pegas K1 = K2 = K3 = 85 N/m.
Ditanya,
Konstanta
pegganti, KP = … ?
ó
KP = K1 + K2 + K3
ó
KP = 85 + 85 + 85
ó
KP = 255 N/m.
Contoh : 2
Tiga
buah pegas masing – masing memiliki konstanta pegas 100 N/m, 200 N/m, dan 400
N/m. Jika ketiga pegas tersebut dirangkai secara seri, maka tentukanlah
konstanta pegas penggantinya.
Pembahasan :
Diketahui,
Konstanta
pegas K1 = 100 N/m, K2 = 200 N/m, dan K3 = 400
N/m.
Ditanya,
Konstanta
pegganti, KS = … ?
Contoh : 3
Dua
buah pegas yang memiliki konstanta pegas 100 N/m dan 400 N/m disusun secara
seri kemudian susunan tersebut diberikan beban yang bermassa 500 gram dengan
cara digantungkan pada bagian bawahnya. Tentukanlah :
a. Konstanta pegas
pengganti
b. Pertambahan panjang
sistem pegas
Pembahasan :
Diketahui,
Pegas
pertama (K1 = 100 N/m)
Pegas
kedua (K2 = 400 N/m)
Massa,
m = 500 gram = 0,5 kg
Ditanya,
a. Konstanta pegganti, KS
= … ?
b. Pertambahan panjang
sistem pegas, Δx = … ?
Penyelesaian
bagian a)

Penyelesaian
bagian b)
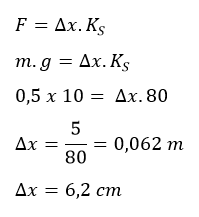
Contoh : 4
Tentukanlah
pertambahan panjang sistem pegas bila dua buah pegas yang memiliki konstanta
pegas masing – masing 200 N/m dan 500 N/m disusun secara seri dan diberi beban
m = 1kg.
Pembahasan :
Diketahui,
Pegas
pertama (K1 = 200 N/m) dan pegas dua (K2 = 500 N/m)
Massa
beban, m = 1 kg.
Ditanya,
Pertambahan
panjang sistem pegas, Δx = … ?
Contoh : 5
Tiga
buah pegas identik disusun secara paralel dan diberi beban sebesar 30 N yang
digantung pada ujung bagian bawah pegas. Jika beban menyebabkan sistem pegas
bertambah panjang 10 cm, maka tentukanlah konstanta masing – masing pegas.
Pembahasan
:
Diketahui,
Tiga
buah pegas identik berarti
K1
= K2 = K3 = K dan disusun paralel.
Beban,
w = F = 30N
Pertambahan
panjang sistem, Δx = 10 cm = 0,1 m
Ditanya,
Nilai
konstanta pegas, K = … ?
Peny
:
Maka
nilai kosntanta masing – masing pegas,
Latihan :
Soal : 1
Sebuah sistem pegas
yang terdiri dari 5 buah pegas yang disusun secara seri diberi beban 0,5 kg
dibagian ujung bawahnya sehingga mengalami pertambahan panjang sebesar 12,5 cm.
Jika kelima pegas tersebut identik sehingga memiliki konstanta yang sama besar,
maka tentukanlah konstanta masing – masing pegas.
Soal : 2
Seorang murid ingin
membuat sistem pegas yang terdiri dari dua pegas untuk menahan beban sebesar 2
kg. Ia memiliki sebuah pegas dengan konstanta 400 N/m dan satu pegas lagi
sedang ia pilih. Jika pertambahan panjang sistem pegas yang diperoleh adalah 10
cm, maka tentukanlah konstanta pegas lainnya yang dibutuhkan murid tersebut.
Soal : 3
Tiga buah pegas
disusun seri – paralel dan di bagian bawahnya digantungi beban seberat W
seperti gambar di bawah ini.
Jika ketiga pegas tersebut memiliki konstanta
yang sama 200 N/m dan mengalami pertambahan panjang 2 cm, maka tentukanlah berat beban yang digantungkan.
Soal : 4
Empat buah pegas
identik disusun secara seri – paralel seperti gambar di bawah ini.
Jika konstanta masing – masing pegas adalah
500 N/m dan beban 40N, tentukanlah pertambahan panjang sistem.
Soal : 5
Dua buah pegas yang
memiliki konstanta berbeda diberi beban yang sama berat yaitu 20N. Jika pegas
pertama memiliki konstanta pegas 200 N/m sedangkan pegas kedua memiliki
konstanta pegas 300 N/m, maka tentukanlah perbandingan pertambahan panjang
pegas pertama dibanding pegas kedua.