Nama Sekolah :
Mata Pelajaran : Fisika
Bahan Ajar : Latihan OSN Fisika
Hari/tanggal :
Waktu :
Soal : 1
Sebuah benda bermassa m diletakkan pada bidang miring
kasar dan dihubungkan ke sebuah benda bermassa M yang menggantung menggunakan
sebuah katrol yang tak bermassa. (lihat gambar).
Sudut θ dengan kemiringan sedemikian sehingga sin θ = 0,6. Koefisien gesekan statis antara m dan bidang miring μs = 0,2. Tunjukkan bahwa kesetimbangan adalah hanya mungkin terjadi jika M terletak diantara dua nilai M1 dan M2. Tentukan nilai M1 dan M2 dalam bentuk m.
Pembahasan :
Tinjau benda bermassa m, yang melakukan
pendakian menuju puncak bidang miring.
Perhatikan gaya – gaya yang bekerja pada benda m.
Pada sumbu y :
Setelah mendapatkan nilai gaya normal N, selanjutnya kita dapat menghitung nilai gaya gesek statis fs.
Jika tegangan tali kendor (Tmin) berarti benda m akan meluncur ke bawah dengan percepatan a. Tetapi sebaliknya jika tegangan tali maksimum (Tmax) berarti sistem dalam keadaan setimbang.
Untuk Tmin :
Untuk Tmax :
Tinjau benda M, dimana gaya – gaya yang bekerja hanya pada sumbu y
saja.
Kita substitusikan pers (3) dan pers (4),
Sehingga kita memperoleh nilai T sbb:
Nilai sin θ = 0,6 maka nilai cos θ = 0,8. (ingat rumus identitas trigonometri 1 = sin2
θ + cos2 θ).
Soal : 2
Perhatikan gambar di bawah ini,
Grafik di atas melukiskan percepatan benda sebagai fungsi waktu. Bila pada keadaan mula – mula benda berkecepatan 4 m/s, besar kecepatan benda pada saat t = 15 sekon adalah ….
A.
12 m/s
B.
25 m/s
C.
40 m/s
D. 64 m/s
E.
70 m/s
Pembahasan :
Untuk grafik a – t di atas,
Dari gambar di atas dapat kita gunakan persamaan
berikut.
Dapat kita hitung v0 kecepatan saat awal dan
sama saja dengan menghitung luas daerah dalam selang waktu (0,t).
Maka kecepatan saat t = 15 detik dapat kita hitung
dengan rumus.
Soal : 3
Seseorang berjalan menuruni sebuah tangga eskalator
yang sedang bergerak turun dan memerlukan waktu 1 menit. Jika kecepatan
berjalannya diduakalikan maka diperlukan waktu 40 detik. Berapakah waktu yang
diperlukan jika orang tersebut relaks (diam) ?
(Soal seleksi OSN 2006 Tingkat Kabupaten/Kota)
Pembahasan :
Karena orang dan eskalator mengarah turun, maka arah
menurun kita anggap arah positip. Eskalator bergerak terhadap tanah dan orang
bergerak terhadap eskalator.
Misalkan,
Kecepatan eskalator terhadap tanah = V1.
Kecepatan orang terhadap eskalator = V2.
Kecepatan orang terhadap tanah = V3.
Waktu menuruni eskalator, t1 = 1 menit = 60
detik.
Panjang eskalator = L
Jika kecepatan orang terhadap eskalator didua kalikan V2’ = 2V2 maka waktu yang diperlukan t2 = 40 detik.
Kita substitusikan persamaan (1) dengan (2)
Substitusikan persamaan (3) ke (1) maka kita peroleh persamaan ke – 4.
Maka waktu t3 saat orang diam saja di atas eskalator. Berarti kecepatan orang terhadap eskalator V2 = 0.
Jadi waktu yang diperlukan untuk menuruni tangga eskalator jika orang itu relaks (diam) adalah 120 detik = 2 menit.
Soal : 4
Dari suatu titik pada ketinggian h di atas tanah, peluru
A diarahkan dengan kecepatan V pada sudut elevasi θ. Peluru lain B diarahkan dari tempat yang sama dengan
kecepatan V tetapi arahnya ke bawah berlawanan dengan A. Buktikan bahwa ketika
mengenai tanah, jarak antara kedua peluru adalah
Soal : 5
Seorang pemain ski melompat dengan sudut 370
dan kelajuan V0 = 10 m/s, kemudian ia mendarat dan menempuh jarak
sejauh s pada bidang miring (lihat gambar).
Jika sudut kemiringan bidang 450. Tentukan jarak
yang ditempuh (asumsikan g = 10 m/s2 dan sin 370 = 0,6).
(Soal seleksi Olimpiade Fisika tingkat Kabupaten/kota
2006)
Penuntun :
Tinjau sumbu X mendatar dan sumbu Y vertikal. Maka x =
s. cos 450 dan y = – s. sin 450.(Jawaban : s =
22,4√2 meter)






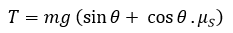



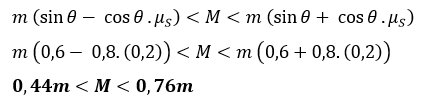













Tidak ada komentar:
Posting Komentar
Silahkan Berkomentar dengan Bijak sesuai dengan semangat kemajuan yang membangun Blog ini dan Jangan keluar dari topik