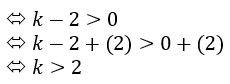Posisi suatu titik T(p,q) terhadap lingkaran L

Posisi suatu titik T(p,q) terhadap lingkaran 

L ≡ x² + y² + Ax + By + C = 0  

Penentuan posisi suatu titik T(p,q) terhadap lingkaran L ≡ x² + y² + Ax + By + C = 0 dilakukan dengan mensubsitusikan T(p,q) ke persamaan lingkaran L.

Maka kita akan memperoleh nilai Kuasa K :

K ≡ p² + q² + Ap + Bq + C  

Dengan melihat nilai K kita dapat menentukan posisi titik T(p,q) terhadap lingkaran.

 

1.     T(p,q) di dalam lingkaran L

 

 

 

 

 

 

 

 

 

 

 

2.     T(p,q) pada lingkaran L

 

 

 

 

 

 

 

 

 

 

 

3.     T(p,q) di luar lingkaran L

 

 

 

 

 

 

Contoh 01:

Diberikan lingkaran dengan persamaan L ≡ x² + y² – 8x – 2y + 8 = 0  serta titik – titik A(5,2),B(4, – 2), dan C(6,4).Hitunglah posisi titik – titik A, B, dan C terhadap lingkaran L.

 

Pembahasan :

 

Untuk titik A(5,2)

 

A(5,2) → (5)² + (2)² – 8(5) – 2(2) + 8 = – 7

 

Kita peroleh nilai K_A = – 7 berarti nilai K_A < 0 , maka titik A

berada di dalam di dalam lingkaran L.

 

Untuk titik B(4, – 2)

Kita peroleh nilai K_B = 0, maka titik B tepat berada di lingkaran L.

 

Untuk titik C(6,4)

Kita peroleh nilai K_C = 4 berarti K_C > 0 , maka titik C berada

di luar dari lingkaran L.

 

Contoh 02:

Tentukan nilai n agar titik T(3, n) terletak pada lingkaran

x² + y² + 5x – 13y + 6 = 0.

 

Pembahasan :

 

Terletak pada lingkaran berarti nilai K_T = 0  

Contoh 03 :

Tentukan nilai k agar titik N(k , 2) terletak di luar lingkaran  

L ≡ x² + y² + 4x – 3y – 10 = 0

 

Pembahasan :

Suatu titik dipastikan berada di luar lingkaran bila K_N > 0

Subsitusikan nilai titik N(k,2) ke dalam persamaan lingkaran

Atau

Latihan

 

1.  Jika titik A(– 5, k ) terletak pada lingkaran L ≡ x² + y² + 2x – 5y – 21 = 0, maka nilai k adalah …

A.   – 2 atau – 1

B.   – 1 atau 6

C.   – 6 atau 1

D.   0 atau 3

E.    2 atau 4

 

2. Titik R(n, 1) terletak di luar lingkaran L ≡  x² + y² – 3x + 2y – 13 = 0, apabila …

A.   Nilai n > 2 atau n < – 5

B.   Nilai n > 5 atau n < – 2

C.   Nilai n > 5 atau n < 2

D.   Nilai – 2 < n < 5

E.    Nilai – 5 < n < 2   

 

3.  Lingkaran L berpusat di (1,3) dan berjari – jari R. Agar titik (5,0) terletak di luar L, maka nilai R haruslah …

A.   R > 5

B.   R > 4

C.   0 < R < 5

D.   4 < R < 5

E.    3 < R < 5

 

4.   Lingkaran L ≡ x² + y² – 2x + 4y – 6 = 0, memotong sumbu x di titik P dan Q, maka panjang PQ adalah …

A.   7√2

B.   5√2

C.   2√5

D.   2√7

E.    4√7

 

5. Titik T(x,y) terletak pada lingkaran L ≡ x² + y² – 6x + 8y = 0, sedangkan R(a,b) titik yang terletak di dalam lingkaran sedemikian sehingga TR = k dengan k konstanta tetap.

Nilai dari 

A.   1

B.   2

C.   3

D.   4

E.    5 

Read More

Soal uraian Teori Kinetik Gas I

Pada kesempatan kali ini saya akan berbagi pengalaman belajar dan mengajar. Untuk Bapak/Ibu guru yang berkenan dapat mengambil soal ini untuk dijadikan naskah soal ulangan atau bahan ajar dengan tujuan untuk evaluasi. Materi yang saya bagikan berupa 15 soal uraian gas ideal dan pada kesempatan lain akan saya bagikan penyelesaiannya juga. Jika ada saran, nantinya bapak/ibu dapat meninggalkannya di kolom komentar, terima kasih. 

Uraian : 

Soal : 1

Sepuluh liter gas ideal yang suhunya 127⁰C mempunyai tekanan 165,6 Pa.Hitung banyak partikel gas tersebut.

Soal : 2

Gas ideal mempunyai volume 100 cm³ saat suhunya 27⁰C dan tekanan 1 atm. Jika suhunya naik menjadi 87⁰C dan tekanannya 2 atm, berapa volume gas sekarang?.

Soal : 3

Sebuah tangki memiliki volume 0,3 m³ dan berisi 2 mol gas helium bersuhu 27⁰C. Hitung :

a)    Energi kinetik rata – rata gas ideal

b)    Energi kinetik total gas ideal

Soal : 4

Tekanan gas ideal dalam bejana tertutup turun menjadi 36% dari keadaan semula. Berapa penurunan kelajuan molekul gas jika kelajuan mula – mulanya 400 m/s ?.

Soal : 5

Suatu gas ideal menempati volume 8 m³ dan tekanan 2,43 x 10⁵ Pa diekspansi secara adiabatik sehingga volumenya menjadi 27 m³. Jika besar tetapan laplace 5/3. Hitung besar tekanan gasnya.

Soal : 6

Dalam sebuah ruang tertutup terdapat gas ideal dengan suhu 27⁰C, tekanan 3 atm, dan volume 8 L. Jika gas dipanaskan sampai suhu 127⁰C, volumenya menjadi tiga kali semula. Berapa besar tekanannya.

Soal : 7

Sebuah tangki berisi gas 50 L dengan massa 2 kg dan tekanan 10 atm. Berapa banyak gas harus ditambahkan ke dalam tangki agar tekanannya menjadi 15 atm.

Soal : 8

Berapa kecepatan rata – rata molekul gas oksigen normal (P = 1 atm), jika massa jenisnya 1,28 kg.m ^{– 3}.

Soal : 9

Kecepatan rata – rata molekul gas nitrogen pada suhu T adalah 487 m/s. Berapa besar suhu gas nitrogen pada saat itu, jika tetapan k = 1,38 x 10 ^{– 23} J.K ^{– 1} dan massa gas nitrogen = 28 sma ( 1 sma = 1,7 x 10 ^{– 27} kg).

Soal : 10

Jika konstanta Boltzman 1,38 x 10 ^{– 23} J.K ^{– 1}, hitung energi kinetik sebuah atom gas helium pada suhu 227⁰C.

Soal : 11

Gas helium mempunyai energi dalam ketika massanya 8 g.Hitung suhu gas itu jika tetapan Boltzman 1,38 x 10 ^{– 23} J.K ^{– 1}.

Soal : 12

Hitung besar energi dalam dari dua mol gas ideal pada suhu 27⁰C.

Soal : 13

Suatu gas ideal dalam keadaan normal mempunyai tekanan 2,4 x 10⁵ Pa. Jika massa jenis gas tersebut 20 kg/m³. Hitung kecepatan efektif gas tersebut.

Soal : 14

Sebuah tangki memiliki volume 300 liter dan berisi 20 mol gas helium bersuhu 27⁰C. Hitunglah :

a) Energi dalam gas helium

b) Energi kinetik rata - rata  per molekul 

Soal : 15

Hitung energi kinetik 1 gram gas helium yang berada dalam tabung bersuhu 27⁰C.(Mr He = 4).

Read More

Pembahasan Soal : 5 (halaman 115/No.12)

Soal : 5 (halaman 115/No.12)

Dua buah katrol dihubungkan dengan tali seperti gambar berikut. 

Persamaan lingkaran dari katrol I adalah x² + y² = 16, dan jarak antara titik pusat katrol I dan II adalah 20 cm.
a.   Tentukan persamaan lingkaran dari katrol II
b.   Jika jari – jari katrol I = r, jarak antara titik pusat katrol I dan II = d, 

    dan sudut yang dibentuk oleh garis singgung persekutuan luar 

    dan garis sejajar sumbu Y yang menyinggung katrol I = q, 

    maka tentukan persamaan katrol II.
c.   Bagaimana persamaan katrol I, jika ukuran katrol II lebih lebih kecil 

    dari pada katrol I ?.
(Nilai max : 40)
 
Bagian a) (Maksimum : 10 point)
 
Catatan, katrol I (lingkaran I) berada di bawah katrol II.
 
Persamaan lingkaran I (katrol I ) :
 
K₁ ≡ x² + y² = r₁²
 
Maka r₁ = 4 cm.

 
Maka kita dapat menentukan jari – jari katrol II.

 
Sehingga jari – jari katrol II,
 
ó r₂ = rs + r₁
ó r₂ = 11,55 + 4
ó r₂ = 15,55 cm
 
Dan titik pusat katrol II, P₂(0,20)
 
Maka persamaan lingkaran (katrol) II,
 
K₂ ≡ (x – a)² + (y – b)² = r₂²
K₂ ≡ (x – 0)² + (y – 20)² = (15,55)²
K₂ ≡ x² + y² – 40y + 400 = 241,709
K₂ ≡ x² + y² – 40y + 400 –  241,709 = 0
 
K₂ ≡ x² + y² – 40y + 158,291 = 0
 
 
Bagian b) (Maksimum : 15 point)
 
K₁ ≡ x² + y² = r₁² dan r₁ = r serta sudutnya = q

Dan jari – jari K₂  dan titik pusat P₂(0,d) : 
r₂ = r₁ + rs  
r₂ = r + d tan q 
K₂ ≡ (x – a)² + (y – b)² = r₂²
K₂ ≡ (x – 0)² + (y – d)² = (r + d tan q)²
K₂ ≡ x² + y² – 2yd + d² = r² + 2rd tan q + d².tan²q
K₂ ≡ x² + y² – 2yd + d² – (r² + 2rd tan q + d².tan²q) = 0
K₂ ≡ x² + y² – 2yd + d² (1– tan² q) – r² – 2rd tan q = 0 
Karena sec² q = 1 – tan² q, maka persamaan lingkaran K₂ menjadi :
 
K₂ ≡ x² + y² – 2yd + d² sec² q – r² – 2rd tan q = 0
 
 
Bagian c) (Maksimum : 15 point)
 
Bagaimana persamaan katrol I ? jika r₂ < r₁ :
Persamaan lingkaran I adalah K₁ = x² + y² = r₁² dan r₁ = r cm.
Sebelum kita lanjutkan, perlu diingat katrol I berada di bawah katrol II.
 

 maka, 

 
Sehingga jari – jari katrol II,
 
ó r₂ = r₁ + qr
 
Dan titik pusat katrol II, P₂(0,– d)
 
Maka persamaan lingkaran (katrol) II,
 
K₂ ≡ (x – a)² + (y – b)² = r₂²
 
K₂ ≡ (x – 0)² + (y + d)² = r₂²
 

 

Read More

Pembahasan Soal : 4 (halaman 115/No.11)

Soal : 4 (halaman 115/No.11)

Tentukan persamaan lingkaran yang berpusat di (1,–3) serta menyinggung garis g  8x – 6y + 10 = 0.

(Nilai max : 15)

 

Jawaban,

Jarak titik (a,b) ke garis Ax + By + C = 0

 

Persamaan garis 8x – 6y + 10 = 0

 

Persamaan lingkaran :

 

L ≡ (x – a)² + (y – b)² = r²

 

Read More