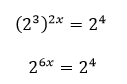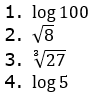Tujuan Instruksional Utama (TIU)
Siswa memahami berbagai sistem bilangan serta dapat
menerapkannya baik dalam Matematika, mata pelajaran lain,
maupun dalam
kehidupan sehari – hari.
Daftar Isi :
PANGKAT TAK SEBENARNYA
(Fungsi dan Persamaan Eksponen/Logaritma)
1. Pangkat tak sebenarnya
1.1.
Eksponen Bulat Positip
1.2.
Eksponen Bulat Negatip dan Nol
1.3.
Eksponen Rasional
2. Bilangan Irasional dan Bentuk Akar
2.1.
Menyederhanakan Bentuk – Bentuk Akar
2.2.
Merasionalkan Penyebut Pecahan
1. Pangkat Tak Sebenarnya
Istilah “Bilangan berpangkat” dipergunakan untuk bilangan yang
ditulis
dalam bentuk an . Dimana a merupakan bilangan pokok
dan n merupakan
bilangan pangkatnya. Bilangan pokok
pada bilangan berpangkat merupakan anggota
bilangan real.
Sedangkan bilangan pangkatnya (eksponen) boleh bernilai
negatip,
nol, dan positip.
Sifat – sifat dasar bilangan berpangkat.
1.1. Eksponen Bulat Positip
1.2. Eksponen Bulat Negatip dan Nol
1.3. Eksponen Rasional
Dengan mengasumsikan
bahwa semua sifat – sifat
dasar yang berlaku pada bilangan berpangkat positip
berlaku juga pada bilangan berpangkat rasional.
Contoh : 1
Perhatikan bilangan
berpangkat a1/2 sama dengan …
Contoh : 2
Perhatikan bilangan
berpangkat a3/2 sama dengan …
Contoh soal :
Conso : 1
Persamaan (8x)2 = 16, hanya dipenuhi jika x sama
dengan …
A. ½
B. 2
C. 1½
D. 2/3
E. ¼
Pembahasan 1 :
Terlihat
sisi kanan dan kiri memiliki bilangan faktor 2,
dimana 8 bisa dibagi 2 dan 16
juga bisa dibagi dengan 2.
Bilangan pokok 2 yang berada di kedua sisi kanan dan kiri,
kita coret.
Sehingga terbentuk persamaan berikut ini.
Kunci : D
Conso : 2
Harga x yang memenuhi persamaan
adalah …
A. 2
B. 5
C. 9/5
D. – 9/5
E. 2/5
Pembahasan 2 :
Perhatikan persamaan di atas, kedua sisinya kita ubah
menjadi persamaan
berpangkat yang memiliki basis
(bilangan pokok) 2.
Kunci : D
2. Bilangan Irasional dan Bentuk
Akar
Kita telah
mempelajari sistem – sistem bilangan berikut.
1. Sistem bilangan Asli, A = {1,2,3,..}
2. Sistem bilangan Cacah, C = {0,1,2,3,…}
3. Sistem bilangan Bulat, B = {…, - 2, - 1, 0, 1, 2, …}
4. Sistem bilangan Rasional Q yang terdiri dari atas
himpunan bilangan bulat dan himpunan bilangan pecahan.
5. Sistem bilangan real R
Semua sistem bilangan di atas tertutup operasi penjumlahan
dan perkalian. Dan juga berlaku hukum – hukum komutatif dan
asosiatif pada operasi
penjumlahan dan perkalian.
Serta hukum distributif perkalian terhadap
penjumlahan.
Di bawah ini diagram venn yang memperlihatkan hubungan
sistem – sistem
bilangan tersebut di atas.
Bilangan rasional ialah bilangan yang dapat ditulis dalam
bentuk a/b,
dimana b ≠ 0 ; a, b є {bilangan bulat}.
Contoh :
Semua bilangan – bilangan di bawah ini merupakan bilangan
rasional 0, 2,
5, 2/3, 3/8 dan seterusnya. Sebab :
- 0 = 0/1 atau 0/2
- 2 = 2/1 atau 4/2
Dan seterusnya.
Bilangan Irasional adalah bilangan real yang tidak merupakan
bilangan
rasional, yaitu bilangan – bilangan yang tidak dapat
ditulis dalam bentuk a/b.
Conso : 3
Di bawah ini yang merupakan bilangan rasional
Pernyataan
yang benar ….
A. 1,
2, dan 3
B. 1
dan 3
C. 2
dan 4
D. hanya
4
E. semua
benar
pembahasan 3 :
Maka
pernyataan yang benar (1) dan (3).
Kunci : B
2.1. Menyederhanakan bentuk – bentuk
akar
√a x √b = √ab, a >
0 dan b > 0
Contoh :
Sederhanakan √32
Pembahasan :
= √32
= √16 x √2
= 4 x √2
= 4√2
Contoh :
Sederhanakan √588
Pembahasan :
=√588
=√72 x 22
x 3
=14√3
Contoh :
Sederhanakan 2√3 -
5√3 + 7√3
Pembahasan :
= 2√3 - 5√3 + 7√3
= (2 – 5 + 7 )√3
= 4√3
Contoh :
Sederhanakanlah √2 x
√6
Pembahasan :
= √2 x √6
= √12
= √4 x 3
= 2√3
Contoh :
Sederhanakanlah √2(3
- 2√2)
Pembahasan :
= √2(3 - 2√2)
= 3√2 – (2√2)√2
= 3√2 – 4
Contoh :
Sederhanakanlah (√2 -
√3)(√2 + √6)
Pembahasan :
= (√2 - √3)(√2 + √6)
= √2.√2 + √2.√6 -
√2.√3 - √3.√6
= √4 + √12 - √6 - √18
= 2 + 2√3 - √6 - 3√2
= 2(1 + √3) - √6 -
3√2
2.2. Merasionalkan penyebut pecahan
2.2.1.
Bentuk
Contoh :
Rasionalkan penyebut
pecahan dari
2.2.2.
Bentuk
Contoh :
Rasionalkan
penyebut pecahan
2.2.3.
Bentuk
Contoh :
Rasionalkanlah
penyebut pecahan dari