Dinamika Gerak 2 Untuk UM PTN

DAFTAR ISI :

1.  TEORI

2.  CONTOH SOAL

2.1.    Gaya sejajar bidang datar

2.2.    Gaya membentuk sudut

2.3.    Gaya menggunakan katrol

2.4.    Gaya pada bidang miring

2.5.    Gaya kontak dua benda

 

 

1. TEORI 

 

Dinamika Gerak melibatkan gaya gesek dalam beberapa kasus gerak dinamika, variasi menentukan nilai gaya normal, gaya kontak dan penguraian gaya – gaya.

 

Hukum Newton I

ΣF = 0

Berarti benda dalam

·        keadaan diam atau

·        bergerak dengan kecepatan konstan/tetap

·        lintasan lurus (GLB)

·        nilai percepatannya sama dengan nol (a = 0).

Hukum Newton II

ΣF = m.a

Berarti benda

·        bergerak dengan percepatan tetap (a ≠ 0).

·        bergerak lurus berubah beraturan (GLBB).

·        Kecepatan benda berubah – ubah (v ≠ 0)

Gaya gesek, f_g

Gaya gesek antara dua buah benda atau lebih yang bersinggungan langsung. 

f_g = N. μ

 gesekan antara benda dapat terjadi saat diam atau bergerak dengan kecepatan tetap f_s (f_s = N.μ_s ). Dan gesekan antara benda dapat juga terjadi tatkala sedang bergerak f_k ( f_k = N.μ_k ).

Koefisien gesekan μ merupakan tingkat kekasaran permukaan yang bersinggungan langsung. Bernilai antara nol hingga kurang dari satu ( 0 ≤ μ < 1). Perlu diingat selalu μ_s > μ_k, dan jika μ = 0 itu artinya bidang yang bersinggungan sangat licin. Serta tidak akan pernah nilai koefisien gesekan sama dengan 1 (μ ≠ 1).

 

2. CONTOH SOAL

 

Contoh : 1

Perhatikan gambar berikut ini.

Benda bermass m = 10 kg berada di atas lantai yang kasar kemudian ditarik dengan gaya F = 12N ke arah kanan. Jika koefisien gesekan statis antara benda dan lantai adalah 0,2 dan koefisien gesekan kinetis 0,1. Tentukan :

a)  Gaya normal

b) Gaya gesek antara benda dan lantai

c)  Percepatan gerak benda

 

Pembahasan :

 

Bagian a)

tinjau sumbu y,

Bagian b)

 

Gaya gesek antara benda dengan lantai, f :

Gaya gesek statis, f_s :

 

 

 

Gaya gesek kinetis, f_k :

 

 

 

Bagian c)

 

Untuk menentukan percepatan benda, kita tinjau  gaya – gaya yang bekerja pada sumbu x. Dan kita dapati F < f_s ( F = 12 N dan f_s = 20N), berarti benda masih dalam keadaan diam. Lalu kita simpulkan benda tidak bergerak a = 0.

 

 

Contoh : 2

Perhatikan gambar berikut!

 

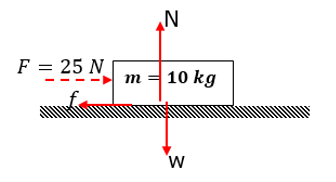
Awalnya benda diam, kemudian diberikan gaya F yang arahnya ke kanan. Jika koefisien gesekan antara permukaan lantai dengan bagian bawah benda secara berturut – turut 0,2 dan 0,1. Maka tentukan :

a)  Gaya normal

b) Gaya gesek antara benda dengan lantai

c)  Percepatan benda

d) Jarak benda setelah 2 sekon

 

Pembahasan :

 

Bagian a)

Tinjau sumbu y,

Bagian b)

 

Gaya gesek antara benda dengan lantai, f :

Gaya gesek statis, f_s :

Gaya gesek kinetis, f_k :

Bagian c)

 

Dari nilai gaya gesek yang kita peroleh dari bagian b), kemudian bandingkan F dengan gaya gesek benda. F = 25 N dan f_k = 10N serta f_s = 20 N, F > f_s berarti benda bergerak dari diamnya.

 

Bagian d)

 

Contoh : 3

Perhatikan gambar di bawah ini,

Sebuah benda bermassa 10 kg, mula – mula dalam keadaan diam. Jika sudut yang terbentuk antara gaya F = 25N dengan garis mendatar adalah 37⁰. Dan koefisien gesek kinetis permukaan lantai adalah 0,1 dan percepatan gravitasi bumi g = 10 m.s ^{– 2} .

 Tentukanlah :

a)  Gaya Normal

b) Gaya gesek

c)  Percepatan gerak benda

(jika sin 37⁰ = 0,6 dan cos 37⁰ = 0,8)

 

Pembahasan :

Bagian a)

 

Tinjau sumbu y :

 

Bagian b)

Besar gaya gesek kinetis, f_k :

 

Bagian c)

 

Percepatan benda, a_x :

Contoh : 4

Perhatikan gambar berikut!

Sebuah benda bermassa 100 kg dilepaskan dari puncak bidang miring dari keadaan diam. Koefisien gesek bidang miring 0,125 dan percepatan gravitasi bumi g = 10 m.s^{- 2} serta sin 53⁰ = 0,8 dan cos 53⁰ = 0,6. 

Tentukan :

a)  Besar gaya normal pada balok

b) Gaya gesek antara balok dengan bidang miring

c)  Besar percepatan balok

 

Pembahasan :

 

 

Bagian a)

 

Besar gaya normal, N :

 

 

Bagian b)

 

Besar gaya gesek, f_k :

 

 

Bagian c)

Contoh : 5

Balok A bermassa 40 kg dan balok B bermassa 20 kg berada di atas permukaan licin yang datar. Kemudian balok A dikenai gaya F sebesar 120 N, seperti gambar berikut.

 

Tentukan :

a)  Percepatan gerak kedua balok

b) Gaya kontak antara balok A dan B

 

Pembahasan :

Bagian a)

Asumsikan kedua balok A dan B merupakan suatu sistem.

Bagian b)

 

Contoh : 6

Balok A dan B terletak pada permukaan bidang miring didorong oleh gaya F sebesar 480N seperti gambar berikut ini.

Tentukan :

a)  Percepatan gerak kedua balok

b) Gaya kontak antara balok A dan B

 

Pembahasan :

 

Bagian a)

 

Untuk menghitung besar percepatan benda, lukiskan terlebih dahulu semua gaya yang bekerja. Kemudian perhatikan dari soal, tidak ada disebutkan koefisien gesekan. Itu berarti gaya gesek dapat kita abaikan.

 

Bagian b)

Untuk menentukan gaya kontak antara balok A dan B (F_AB), mari kita gambar ulang gaya – gaya yang bekerja.

 

Contoh : 7 (UMPTN 1993)

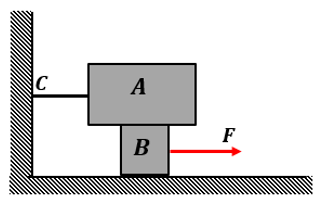
Perhatikan gambar berikut!

Balok A beratnya 100N diikat dengan tali mendatar di titik C. Balok B beratnya 500N, koefisien gesekan antara A dan B sama dengan 0,2 dan koefisien antara B dengan lantai sama dengan 0,5. Maka besarnya gaya F minimal untuk menggeser balok B.

A.  950 N               D. 320 N

B.  750 N               E. 100 N

C.  600 N

 

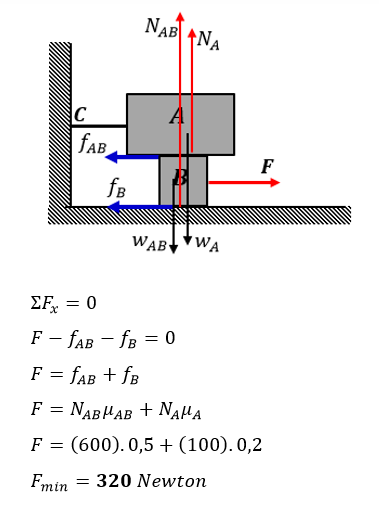
Pembahasan :

 

Lukiskan semua gaya yang bekerja pada sistem.

Contoh : 8

Benda pertama dengan massa m₁ = 6 kg dan benda kedua bermassa m₂ = 4 kg dihubungkan dengan katrol seperti gambar di bawah ini.

Jika lantai licin dan m₂ ditarik dengan gaya F = 42 N.

Tentukan :

a)  Percepatan benda pertama

b) Percepatan benda kedua

c)  Tegangan tali T  

 

Pembahasan :

 

Bagian a)

 

Tinjau benda m₂ :

 

Tinjau benda m₁ :

Sebagai catatan,

(1)      Lantai licin, berarti tidak akan ada gaya gesek

(2)      Percepatan kedua benda a₁ = 2a₂.

 

Selanjutnya kita substitusikan pers (2) ke dalam pers (1)

 

Bagian b)

Menentukan percepatan benda m₂.

Bagian c)

Untuk menentukan besar tegangan tali (T), cukup memilih salah satu persamaan (1) atau (2).

Contoh : 9

Massa A = 4 kg dan massa B = 6 kg dihubungkan dengan tali dan ditarik dengan gaya F = 40N ke kanan dengan sudut 37⁰ terhadap horizontal. (cos 37⁰ = 0,8 dan sin 37⁰ = 0,6).

Jika koefisien gesek kinetis kedua benda dengan lantai 0,1. 

Tentukan :

a)  Percepatan gerak kedua benda.

b) Tegangan tali penghubung kedua benda A dan B.

 

Pembahasan :

 

Bagian a)

 

Tinjau benda B dan lukiskan gaya – gaya yang bekerja pada benda B.

Tinjau gaya pada sumbu y :

 

 

Tinjau gaya pada sumbu x :

Tinjau benda A :

Tinjau gaya – gaya pada sumbu y

Tinjau gaya – gaya pada sumbu x

Ketika benda B bergerak, maka benda A juga spontan ikut bergerak. Itu berarti percepatan a_A = a_B , lalu kita asumsikan besarnya sama (a_A = a_B = a).

Bagian b)

Untuk menentukan nilai tegangan T, maka kita substitusikan nilai a ke salah satu persamaan (1) atau (2).

Contoh : 10

Perhatikan gambar berikut!

Jika massa tali dan katrol diabaikan serta bidang miringnya licin. Tentukan :

a)  Percepatan gerak kedua benda

b) Tegangan tali penghubung kedua benda

 

Pembahasan :

 

Dengan asumsi kedua benda A dan B merupakan suatu sistem. Sehingga sistem akan bergerak ke arah benda B, sebab m_B > m_A. Dan kedua sisi bidang miring licin, maka gaya gesek pada kedua bidang miringnya dapat kita abaikan.

Bagian a)

  

Tinjau benda B,

Tinjau benda A,

Lalu kedua persamaan kita substitusikan saja.

Bagian b)

 

Untuk menghitung nilai tegangan tali T,

Contoh : 11

Perhatikan gambar di bawah ini.

Massa balok A = 6 kg, massa balok B = 4 kg dan koefisien gesekan kinetis antara balok A dengan B sama dengan 0,1. Koefisien gesekan antara balok A dengan lantai sama dengan 0,2. Tentukan besar gaya F agar balok A bergerak lurus beraturan ke kanan, abaikan massa katrol dan tali.

 

Pembahasan :

 

Tinjau benda B

Tinjau benda secara keseluruhan AB,

Contoh : 12

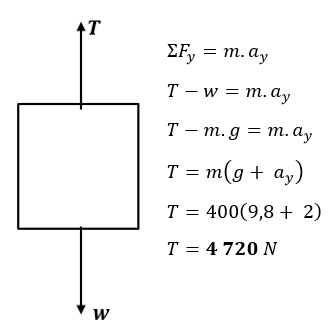
Sebuah elevator bermassa 400 kg bergerak vertikal ke atas dari keadaan diam dengan percepatan tetap 2 m.s ^{– 2}. Jika percepatan gravitasi g = 9,8 m.s ^{– 2} , maka tegangan tali penarik elevator adalah …

A.   400 N               D. 3 920 N

B.   800 N               E. 4 720 N

C.   3 120

 

Pembahasan :

Contoh : 13

Perhatikan gambar di bawah ini.

Koefisien gesekan kinetis antara massa pertama dengan lantai 0,1. Massa benda pertama 4 kg dan massa kedua 6 kg, tentukan :

a)  Percepatan gerak benda pertama

b) Percepatan gerak benda kedua

 

Pembahasan :

 

Bagian a)

Dari gambar terlihat m₂ > m₁ maka sistem akan bergerak searah benda m₂.

Karena a₁ = 2a₂ , lalu substitusikan pers (1) ke dalam pers (2).

Bagian b)

 

 

Contoh : 14

Balok m bermassa 10 kg menempel pada dinding kasar dengan koefisien gesekan kinetis 0,1. Balok mendapat gaya horizontal F₂ = 50 N dan gaya vertikal F₁. 

Tentukan besar gaya F₁ agar balok bergerak vertikal ke atas dengan percepatan 2 m/s².

 

Pembahasan :

Contoh : 15 (UM UGM 2009)

Benda bermassa 4 kg diberi kecepatan awal 10 m/s dari ujung bidang miring seperti ditunjukkan pada gambar di bawah ini.

Benda mengalami gaya gesek dari bidang sebesar 16N dan sin α = 0,85. Benda berhenti setelah menempuh jarak …

A.  3 meter             D. 6 meter

B.  4 meter             E. 8 meter

C.  5 meter

 

Pembahasan :

Benda menaiki bidang miring,

Karena F = 0,

Kunci : B 

Read More

PERTEMUAN - 2 ARUS LISTRIK dc

SEKOLAH                      : …………………………

TAHUN PELAJARAN   : …………………………

MATA PELAJARAN      : …………………………

KELAS                             : …………………………

HARI/TANGGAL           : …………………………

WAKTU                           : …………………………

1)Hukum ohm

“Kuat arus dalam suatu rangkaian sebanding dengan tegangan pada ujung – ujung rangkaian dan berbanding terbalik dengan hambatan rangkaian”.

Grafik :

Rangkaian Percobaan Ohm :

Kode warna :

Resistor ada dua model, resistor tetap (fixed resistor) dan resistor tidak tetap (variable resistor). Yang dimaksudkan model di sini adalah nilai-nya, ada resistor yang bernilai tetap dan ada resistor yang bernilai tidak tetap.

Untuk resistor yang bernilai tetap biasanya menggunakan kode warna, ada yang memiliki empat kode warna dan lima kode warna. Namun disini kita hanya membahas resistor yang memiliki empat kode warna. Sedangkan resistor dengan lima kode warna silahkan anda cari sebagai tugas mandiri.

 

Tugas Mandiri : Cari Tabel Kode warna Resistor 

 

Contoh 01 : (Menentukan nilai resistor berasarkan kode warna)

Misalkan sebuah resistor memiliki kode warna Merah – Merah – Merah

– Emas. Maka nilai resistor tersebut adalah …

 

Penyelesaian :

Nilai Resistor:

R = Merah – Merah – Merah – Emas

Resistor tidak tetap (Variable Resistor) :

Potensiometer 50K

Jika pada 50K pada potensiometer, nilai resistor berubah dari 0 Ω (minimum) hingga nilai 50 kΩ (maksimum).

2)Hambatan Jenis

Dimana :

Dari persamaan (4) dapat disimpulkan : hambatan bergantung pada jenis kawat penghantarnya (ρ), panjang kawat (l), dan berbanding terbalik dengan luas penampangnya (A).

Dimana :

2. Alat ukur Arus dan Tegangan ac

Alat ukur kuat arus listrik adalah Amperemeter dan alat ukur tegangan disebut Voltmeter. Baik Amperemeter dan Voltmeter DC, hasil pembacaannya merupakan nilai rata – rata. Sedangkan amperemeter AC maupun voltmeter AC tidak mengukur nilai rata – rata, karena nilai rata – rata AC sama dengan nol. Sebagai gantinya hasil pembacaan kedua alat ukur besaran listrik tersebut dinyatakan sebagai nilai efektif.

BACA : SERI - 9 RANGKAIAN RLC  

Contoh 02:

Arus DC 3,0 Ayang melalui suatu resistor R membangkitkan daya dissipasi W pada resistor. Berapakah daya dissipasi yang dibangkitkan pada resistor R jika digunakan AC dengan arus maksimum yang terbaca pada osiloskop adalah 3A.

 

Pembahasan :

Daya dissipasi pada arus DC :

Daya dissipasi pada arus AC :

Karena

 

 

 

Contoh 03 :

Arus sinusoidal dengan nilai maksimum 6A mengalir melalui sebuah resistor 5Ω. Tentukan daya rata – rata yang didissipasikan pada resistor.

 

Pembahasan :

Diketahui :

Arus maksimum, i_m = 6A ; Resistor, R = 5Ω

 

Ditanya : Daya dissipasi rata – rata, P = … ?

Penyelesaian :

BACA : PERTEMUAN - 3 GRAVITASI NEWTON

Read More