Ukuran Pemusatan dan Peyebaran Data Berkelompok
1. Nilai rataan hitung
2. Metode Biasa
3. Metode Simpangan Rata – rata
4. Metode Coding
5. Modus
6. Statistik lima serangkai
7. Median dan Kuartil data Tunggal
8. Jangkauan
9. Median dan Kuartil
10. Desil
11. Rataan Simpangan
12. Simpangan Baku
Jika f1 bilangan yang mempunyai rataan
hitung m1, f2 bilangan yang mempunyai rataan hitung m2,
…, dan fn bilangan yang mempunyai rataan hitung mn,
rataan hitung dari keseluruhan bilangan itu, yaitu (f1 + f2
+ … + fn) bilangan, ditentukan oleh formula:
Metode Biasa
Median dan kuartil data tunggal
a. Median data tunggal
b. Kuartil data tunggal
Kuartil adalah
nilai – nilai yang membagi statistik peringkat menjadi empat bagian yang sama
seperti pada gambar di bawah ini.
Jangkauan
a. Jangkauan dan koefisien jangkauan
b. Jangkauan antarkuartil
c. Jangkauan semi antarkuartil
d. Langkah (L)
Atau
e. Pagar dalam (PD) dan pagar luar (PL)
PD = BPB = Q1 – L dan PL = BPA = Q3
+ L
Median dan Kuartil dari data pada tabel
distribusi penentuan median, kuartil bawah, dan kuartil atas pada distribusi
frekuensi dapat dilakukan melalui formula berikut ini :
Desil
a. Data Tunggal
Letak desil ke – i,
Dengan i = 1, 2,
…, 9 dan n = banyak data
(n > 10).
b. Data Berkelompok
Penentuan nilai
desil ke – i dari data berkelompok dapat dilakukan dengan menggunakanformula :
Apabila data
berupa bilangan – bilangan : x1, x2, …, xn dengan frekuensi masing – masing f1,
f2, …, fn, maka rataan simpangan ditentukan menggunakan
formula :
a. Kondisi 1 :
b. Kondisi 2 :
Apabila data berupa bilangan – bilangan : x1,
x2, …, xn dengan frekuensi masing – masing : f1,
f2, …, fn maka simpangan baku (S) ditentukan menggunakan
formula :
c. Jika simpangan baku = S, maka variansi = S2. Varaiansi sering
juga disebut ragam.















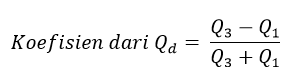












Komentar
Posting Komentar
Silahkan Berkomentar dengan Bijak sesuai dengan semangat kemajuan yang membangun Blog ini dan Jangan keluar dari topik