Tujuan Instruksional
Umum (TIU)
Melalui
pengamatan siswa mengenal pengertian sifat – sifat dan rumus – rumus tentang
lingkaran serta mampu menerapkannya baik dalam bentuk Matematika, dalam mata
pelajaran lain bahkan dalam kehidupan sehari – hari.
BANGUN DATAR :
LINGKARAN
1.
Unsur – Unsur
Lingkaran dan Simetri Pada Lingkaran
Banyak benda – benda di sekitar kita yang
diperoleh karena perputaran. Banyak pula benda – benda yang berputar pada
porosnya atau pada pusatnya.
1.1
Busur Lingkaran
Gambar 2, menunjukkan sebuah lingkaran yang
berpusat di O. Kurva pada keliling lingkaran yang menghubungkan titik A dan
titik B seperti tergambar disebut busur lingkaran.
Apabila sudut pusat yang dihadapi kurang dari
1800 disebut busur pendek (busur
minor). Sedangkan apabila sudut pusat yang dihadapi lebih besar dari 1800
disebut busur panjang (busur mayor).
1.2
Tali Busur Lingkaran
Ruas garis yang menghubungkan titik A dan
titik B disebut tali busur lingkaran. Jadi tali busur adalah ruas garis yang
menghubungkan dua titik pada keliling lingkaran.
Apabila tali busur melalui pusat lingkaran,
maka tali busur tersebut disebut sebagai garis tengah lingkaran (diameter).
Setengah garis tengah lingkaran disebut jari – jari lingkaran.
1.3
Juring Lingkaran
Daerah yang diarsir disebut juring lingkaran.
Sudut ÐROS disebut sudut
pusat. Jadi juring lingkaran adalah daerah yang dibatasi oleh dua buah jari –
jari dan busur lingkaran.
1.4
Hubungan Antara
Busur, Juring, dan Sudut Pusat
Pada suatu lingkaran (beberapa lingkaran yang
mempunyai panjang jari – jari yang sama).
Contoh : 1
Perhatikan gambar di bawah ini,
a) Bila panjang busur CD
adalah 15 cm, tentukanlah panjang busur AB dan BC.
b) Bila luas juring COD
45 cm2, tentukanlah luas juring AOB dan BOC.
Pembahasan
Bagian a)
busur CD = 15 cm
Busur BC
Bagian b)
luas juring COD = 45 cm3
Luas juring BOC
Contoh : 2
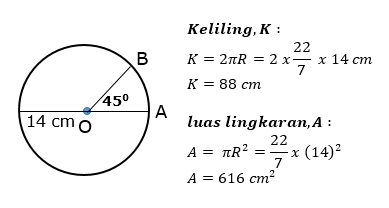
Diketahui titik – titik A dan B terletak
pada keliling lingkaran yang berjari – jari 14 cm dengan sudut AOB = 450.
Tentukanlah :
a) Panjang busur AB
b) Luas juring AOB
Pembahasan
Keliling lingkaran,
Bagian a)
Bagian b)
Contoh : 3
Dua busur AB dan CD pada lingkaran yang
berpusat di titik O, panjangnya 2x cm dan 5x cm. Jika juring luasnya 22 ½ cm2.
Tentukan luas juring AOB.
Pembahasan
Diketahui,
Busur AB = 2x cm
Busur CO = 5x cm
Luas juring = 22 ½ cm2.
1.5
Hubungan Antara
Busur, Sudut Pusat, dan Tali Busur
∆A’OB’ merupakan hasil putaran dari ∆ AOB dengan pusat O.
ó AB = A’B’
ó OP = OP’
ó busur AB = busur A’B’
Berikut ini berlaku bagi sembarang lingkaran,
dua busur dikatakan sama. Jika :
·
Sudut
pusatnya sama besar
·
Tali
busurnya sama panjang
·
Tali
busurnya berjarak sama dari pusat
Apabila dikatakan bahwa tali busur yang sama
panjang memiliki busur yang sama panjang pula, maka harus dipilih pasangan
busur yang sesuai. Artinya kedua – duanya busur pendek atau kedua – duanya
busur panjang.
Contoh : 4
Perhatikan gambar di bawah ini,
Pada gambar di atas, EF dan GH terletak sama
jauh dari pusat O. GHK dan EFK adalah ruas garis dengan KF = KH. Buktikan KE =
KG.
Pembahasan
EF = GH, karena terletak sama jauh dari pusat
O
KF = KH
Maka,
ó KF + EF = KH + GH
ó KF = KG (terbukti)
1.6
Segi Banyak Beraturan
Segitiga, segiempat, segilima, dan seterusnya
semuanya disebut segi banyak. Jika semua sudut dan sisi segibanyaknya tersebut
sama, maka segi banyak itu disebut segibanyak beraturan.
Rumus sudut pusat segi – n beraturan :
Rumus sudut segi – n beraturan :
Contoh : 5
Tentukanlah sudut pusat, sudut alas segitiga
sama sisi, dan sudut segienam beraturan.
Pembahasan
Segienam beraturan diperlihatkan seperti
gambar berikut.
Sudut pusat segienam beraturan,
Sudut alas segitiga sama sisi,
Sudut segi – enam,
Contoh : 6
Tentukanlah sudut segi – 20 beraturan.
Pembahasan
Contoh : 7
Tentukanlah luas segi enam beraturan yang
berjari – jari 6 cm.
Pembahasan
Secara umum dapat ditulis :
Luas segi – n beraturan,
Terima kasih,