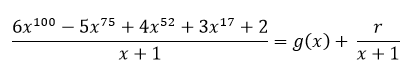SERI - 2 UAS SMA

Sejumlah massa gas m, yang keluar dari lubang suatu dinding silinder yang luasnya A dalam selang waktu singkat t dapat dinyatakan sebagai :  

k adalah tetapan tak berdimensi. P adalah tekanan gas, ρ jenis, dan x, y, dan z adalah eksponen. Maka nilai x, y, dan z berturut – turut adalah …

    Pembahasan :

Lalu kita subsitusikan ke dalam persamaan soal dan sementara waktu 

konstanta (k) pada persamaan soal dapat kita abaikan. 

Kita mulai dari sekon : 

NB: cukup kita ambil eksponennya saja 

Kemudian kita ke kilogram : 

karena kilogram pangkat 1, 

Terakhir meter : 

NB : bilangan berpangkat nol sama dengan 1

Kunci : B 

SERI - 46 UAS MATE (MINAT)

 

Nomor 17

Sisa pembagian x²⁰¹⁴ – Ax²⁰¹⁵ + Bx³ – 1 

oleh x² – 1 adalah   – x + B. 

Maka nilai 2A + B adalah …

A.  1

B.  2

C.  3

D.  4

E.  5

 

Pembahasan :

 

Fungsi yang mau dibagi, P(x) = x²⁰¹⁴– Ax²⁰¹⁵ + Bx³ – 1

 

Fungsi pembagi, g(x) = x²– 1

 

Sisa hasil bagi, S(x) = - x + B

 

Fungsi P(x) = g(x).H(x) + S(x)

 

ó P(x) = ( x² – 1 ).H(x) + ( - x + B )

ó P(x) = ( ( x + 1 )( x – 1 ) ). H(x) – x + B

ó x + 1 = 0  atau ó x – 1 = 0

ó       x = - 1 atau          x = + 1

 

maka hasil kali (( x + 1)(x – 1).H(x)) = 0

 

ó P(x) = - x + B

 

subsitusikan x = - 1 ke persamaan P(x)

 

ó P( - 1 ) = x²⁰¹⁴ – Ax²⁰¹⁵+ Bx³ – 1

 

ó P( - 1 ) = (-1)²⁰¹⁴ – A(-1)²⁰¹⁵ + B(-1)³ – 1

 

catatan, jika pangkat ganjil nantinya nilai minus 

tetap akan menjadi minus juga. 

Beda jika pangkatnya genap, 

tadinya minus berubah menjadi positip.

 

 

 

ó lalu kita samakan P(x) = S(x)

 

ó 1 + A – B – 1 = - ( - 1 )  + B  

 

ó A = 1 + 2B … (1)

 

subsitusikan x = + 1 ke persamaan P(x)

 

ó P( +1) = (+1)²⁰¹⁴ – A(+1)²⁰¹⁵ + B(+1)³ – 1

 

ó lalu kita samakan P(x) = S(x)

 

ó 1 – A + B – 1 = - (+1 )  + B  

 

ó A = 1 … (2)

 

subsitusikan pers (2) ke pers (1)

 

ó 1 = 1 + 2B

ó B = 0

ó maka nilai 2A + B,

ó 2A + B = 2(1) + 0

ó 2A + B = 2

 

Kunci : B

 

 

SERI - 47 UAS MATE (MINAT)

Nomor 18

Hasil bagi dan sisa pembagian x³+ 3x² + 4x – 5

oleh x + 2 adalah ….

A.  Hasil bagi x² + x + 2 dan sisa – 9

B.  Hasil bagi x² + x - 2 dan sisa – 9

C.  Hasil bagi x² - x + 2 dan sisa – 9

D.  Hasil bagi x² + x + 2 dan sisa + 9

E.  Hasil bagi x² - x + 2 dan sisa + 9

 

 

Pembahasan : 

 

HB  : x² + x + 2

S(x) : - 9

 

 

Kunci : A

SERI - 49 UAS MATE (MINAT)

Nomor 19

Jika P(x) = 3x³ – 4x² – ax + 2 habis 

dibagi (3x + 2 ), maka nilai a adalah …

 

A.  – 2

B.  – 1

C.  0

D.  + 1

E.  + 2

 

Pembahasan :

 

Jika anda ingin menyelesaikan soal nomor 19

ini dengan menggunakan metode bersusun, 

silahkan simak caranya di bawah ini. 

Maka nilai a dapat kita tentukan

 

ó (4 – a)x = 3x

ó 4 – a = 3

ó a = 1

Jika anda ingin mempelajari 

penyelesaian soal nomor 19 ini, 

menggunakan metode Bagan Horner.

 

P(x) = 3x³ – 4x² – ax + 2

Pembagi (3x + 2 )

 

ó 3x + 2 = 0

ó 3x = - 2

ó x = - 2/3 

Hasil Bagi, HB : 3x² – 6x – ( a – 4 )

Sisa, S( x ) : 2/3 ( a – 1 )

 

Bentuk S(x) = ax + b => S(-2/3) = a(-2/3) + b 

Kunci : D

SERI - 50 UAS MATE (MINAT)

Pilihan Berganda :

Nomor 20

Jika, 

Maka nilai r = …

 

A.  0

B.  4

C.  14

D.  20

E.  30

 

Pembahasan :

 

BU Teorema Sisa : P(x) = g(x).H(x) + S(x)

 

ó g(x) = x + 1 , g(x) = 0

ó 0 = x + 1

ó x = - 1 

Dari bentuk umum BU, di atas nilai r = S(x)

 

Kunci : C 

SERI - 51 UAS MATE (MINAT)

Soal : 1

Tentukan persamaan lingkaran yang berpusat 

di (0,0) yang mempunyai jari – jari 2√3.

 

Pembahasan :

 

Titik pusat lingkaran ( a = 0, b = 0 )

 

BU : ( x – a )² + ( y – b )² = r²

ó subsitusikan nilai a dan b ke dalam 

BU, maka akan kita peroleh hasilnya

ó x² + y² = r²

ó x² + y² = (2√3)²

ó x² + y² = 12 

SERI - 52 UAS MATE (MINAT)

 

Soal : 2

Tentukan persamaan umum lingkaran 

jika pusat lingkaran tersebut P ( - 1, 3 ) 

dengan jari – jari 3√2.

 

Pembahasan :

 

Titik pusat lingkaran, P( - 1, 3 )

 

BU : ( x – a )² + ( y – b )² = r²

 

ó ( x – (-1))² + ( y – 3 )² = (3√2)²

ó x² + 2x + 1 + y² – 6y + 9 = 18

ó x² + y² + 2x – 6y – 8 = 0

SERI - 53 UAS MATE (MINAT)

SOAL : 3

Tentukan pusat dan jari – jari lingkaran 

untuk persamaan lingkaran 

2x² + 2y² – 8x + 16y + 4 = 0

Pembahasan :

 

Bentuk Umum, BU :

 

x² + y² + Ax + By + C = 0

2x² + 2y² – 8x + 16y + 4 = 0 

Bagi 2, sehingga persamaan lingkaran

menjadi, 

x² + y² – 4x + 8y + 2 = 0

ó titik pusat : 

Maka titik pusat lingkarannya,

ó Radius :