SERI 1 : PERSAMAAN KUADRAT (SMP)
Materi ajar yang saya bagikan, pernah saya ajarkan di tempat les,
Gang Kemala II. Murid lesnya berasal dari Sekolah SMP Hangkesturi
Medan, yang duduk di bangku kelas IX.
Bab 7 Persamaan Kuadrat (Pengayaan)
Nomor : 60
Akar – akar persamaan ax2 + bx + c = 0
adalah x1 dan x2.
Jika x1 + x2 = –
3 dan x12 + x22 = 29, maka nilai
c/a = …
A.
– 10
B.
– 4
C.
– 5/2
D.
2
Pembahasan :
7.7. Menyelesaikan
Soal Cerita
Nomor : 61
Jika (p + 3) cm adalah sisi terpanjang sebuah segitiga
dengan penyikunya
masing – masing p cm dan (p – 3) cm,
maka panjang sisi hipotenusanya adalah …
A.
10 cm
B.
13 cm
C.
15 cm
D. 17 cm
Pembahasan :
Nomor : 62
Diketahui keliling sebuah persegi panjang 70 cm.
Jika luas
persegi panjang itu 300 cm2 maka panjang
diagonal persegi panjang
itu adalah …
A. 34 cm
B. 25 cm
C. 20 cm
D. 17 cm
Pembahasan :
Nomor : 63
Hasil kali dua bilangan ganjil berurutan sama dengan
255.
Selisih kuadrat dari kedua bilangan itu adalah …
A. 64
B. 81
C. 100
D. 121
Pembahasan :
Nomor : 64
Sebuah batu dilemparkan ke atas dengan kecepatan 24
meter
per detik. Tinggi batu setelah t detik ditentukan oleh rumus
h(t) = 24t –
3t2. Pernyataan di bawah ini yang tidak benar
adalah …
A. Batu melayang di atas selama 8 detik
B. Batu mencapai ketinggian 45 m pada detik ke – 3 dan ke
– 5.
C. Batu mencapai ketinggian maksiumum 49 meter
D. Tinggi maksimum dicapai pada t = 4 detik
Pembahasan :
Nomor : 65
Diketahui jumlah suatu bilangan dengan 3 kali
kebalikannya
adalah 4. Selesih kedua bilangan itu adalah …
A. 5
B. 4
C. 3
D. 2
Pembahasan :
Nomor : 66
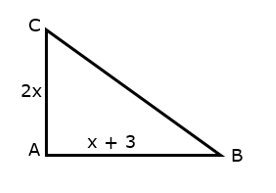
Perhatikan gambar berikut
Jika luas segitiga ABC di atas 54 cm2 maka keliling
segitiga ABC adalah …
A. 27 cm
B. 36 cm
C. 48 cm
D. 60 cm
Pembahasan :
Nomor : 67
Diketahui jumlah kuadrat dua bilangan kelipatan 3
berurutan adalah 225. Jumlah kedua bilangan itu
adalah …
A. 19
B. 20
C. 21
D. 27
Pembahasan :
Nomor : 68
Diketahui x dan y adalah bilangan asli dengan x >
y.
Jika x2 – y2 = 12 maka nilai x + y adalah …
A. 3
B. 4
C. 6
D. 12
Pembahasan :
Nomor : 69
Perhatikan gambar di bawah ini.
Diketahui segitiga ABC siku – siku di C dan CD tegak
lurus
dengan AB. Jika panjang AD =(2x + 1) cm, BD = x cm,
dan CD = 6 cm, maka
panjang BD adalah … cm.
A. 3
B. 4
C. 5
D. 6
Pembahasan :
Nomor : 70
Sebuah prisma dengan alas persegi memiliki rusuk alas
p cm
dan rusuk tegak (p + 5) cm. Jika luas permukaan prisma
114 cm2 ,maka panjang rusuk tegak prisma adalah …
A. 8 cm
B. 7 cm
C. 5 cm
D. 3 cm
Pembahasan :
Nomor : 71
Perhatikan gambar di bawah ini
Diketahui trapesium PQRS siku – siku di P memiliki panjang
PQ = (x + 6) cm, SR = 9 cm, dan PS = (x + 4) cm.
Jika luas trapesium
PQRS 138 cm2, maka keliling trapesium
PQRS adalah …
A. 56 cm
B. 54 cm
C. 52 cm
D. 48 cm
Pembahasan :
Nomor : 72
Diketahui suatu persegi panjang mempunyai panjang
(y +
3) cm dan lebar (7 – y) cm. Luas maksimum
persegi panjang tersebut adalah … cm2.
A. 28
B. 25
C. 24
D. 20
Pembahasan :
Nomor : 73
Suatu persegi panjang mempunyai lebar 3 cm kurang
dari
panjangnya dan luasnya 180 cm2. Keliling persegi
panjang tersebut
adalah … cm.
A. 48
B. 52
C. 54
D. 60
Pembahasan :
Nomor : 74
Luas suatu persegi panjang berukuran panjang (2p + 1)
cm
dan lebar p cm sama dengan luas persegi dengan ukuran sisi
(p + 2) cm. Panjang
sisi persegi adalah … cm.
A. 4
B. 5
C. 6
D. 8
Pembahasan :
Nomor : 75
Jumlah n suku pertama suatu deret aritmatika
ditentukan
dengan rumus Sn = 3n2 – 6n. Jika Sn
= 105 maka banyak
suku bilangan tersebut adalah …
A. 4
B. 5
C. 6
D. 7
Pembahasan :





Komentar
Posting Komentar
Silahkan Berkomentar dengan Bijak sesuai dengan semangat kemajuan yang membangun Blog ini dan Jangan keluar dari topik