Tahun Pelajaran : 2023/2024
Mata Pelajaran : MATEMATIKA (wajib)
Kelas : XII MIA 5
Materi Ajar : Teori Peluang 14
Pilihan Berganda
Soal : 1
Munculnya sisi angka saat pelemparan uang koin adalah …
A. Kejadian pasti
B. Kejadian mustahil
C. Kejadian umum
D. Kejadian acak
E. Lewati
Kunci : D
Soal : 2
Setiap anggota ruang sampel disebut …
A. Kejadian
B. Peluang
C. Titik sampel
D. Uji coba
E. Lewati
Kunci : C
Soal : 3
Ruang sampel adalah …
A. Himpunan bilangan real
B. Himpunan banyaknya jumlah bilangan genap
C. Himpunan semua kemungkinan pada suatu percobaan
D. Himpunan semua kemungkinan pada ujian
E. Lewati
Kunci : C
Soal : 4
Kejadian mustahil dinotasikan sebagai …
A. Nilai P[A] = 0
B. Nilai P[A] = 1
C. Nilai P[A] = 2
D. Nilai P[A] = -
E. Lewati
Kunci : A
Soal : 5
Kejadian pasti dinotasikan …
A. Nilai P[A] = 0
B. Nilai P[A] = 1
C. Nilai P[A] = 2
D. Nilai P[A] = -
E. Lewati
Kunci : B
Soal : 6
Berapa peluang muncul mata dadu berangka ganjil ?
A. 1
B. ½
C. 2
D. 4
E. Lewati
Kunci B
Pembahasan
Ruang sampel pelemparan sebuah dadu S = {1,2,3,4,5,6} sehingga n(S) = 6. Dan kita misalkan kejadian muncul mata dadu berangka ganjil adalah A. Maka A = {1,3,5} sehingga jumlah kejadian A kita
tuliskan n[A] = 3. Itu berarti peluang kejadian A menjadi,
Soal : 7
Berapa peluang muncul mata dadu berangka kurang
dari
3?
A. 1
B. 1/3
C. 3
D. 6
E. Lewati
Kunci : B
Pembahasan
Ruang sampel pelemparan mata dadu untuk 1 kali pelemparan S = {1,2,3,4,5,6} sehingga n(S) = 6. Kejadian muncul mata dadu yang kurang dari 3 dan kita
misalkan kejadiannya B, maka kita tuliskan
B = {1,2} sehingga n(B) = 2. Sehingga peluang kemunculan B :
Soal : 8
Dari satu set kartu bridge, diambil satu kartu secara acak. Berapa peluang mendapatkan kartu As.
A. 1
B. 1/3
C. 3
D. 1/13
E. Lewati
Kunci : D
Pembahasan
Satu set kartu bridge terdiri dari 52 kartu yang
berbeda, maka kita tuliskan n(S) = 52. Di dalam satu set kartu bridge tadi terdapat 4 jenis
kartu As yang berbeda
- Kartu As sekop (hitam)
- Kartu As hati (merah)
- Kartu As daun (hitam)
- Kartu As intan (merah)
Dan setiap jenis kartu berjumlah 13 termasuk salah satunya adalah kartu As tadi. Sehingga kejadian mendapatkan kartu As jenis apa
pun itu kita tuliskan n(A) = 4.
Maka peluang untuk mendapatkan 1 kartus As dalam satu kali penarikan dapat kita tentukan.
Soal : 9
Dari satu set kartu bridge diambil satu kartu secara acak. Berapa peluang mendapatkan kartu berwarna hitam.
A. 1
B. ½
C. 2
D. 1/12
E. Lewati
Kunci : B
Pembahasan
Satu set kartu bridge terdiri dari 52 kartu yang
berbeda, maka kita tuliskan n(S) = 52. Di dalam satu set kartu bridge tadi terdapat 4 jenis
kartu yang berbeda.
- Kartu sekop (hitam) = 13 jenis
- Kartu hati (merah) = 13 jenis
- Kartu daun (hitam) = 13 jenis
- Kartu intan (merah) = 13 jenis
Terlihat jenis kartu berwarna hitam yakni sekop dan daun dengan jumlah = 26. Kejadian munculnya kartu berwarna hitam n(A) = 26.
Maka dapat
kita hitung peluang mendapatkan kartu hitam.
Soal : 10
Dari satu set kartu bridge diambil satu kartu secara acak. Maka berapa peluang mendapatkan kartu bergambar.
A. 1
B. 1/3
C. 1/13
D. 3/13
E. Lewati
Kunci : D
Pembahasan
Satu set kartu bridge terdiri dari 52 kartu yang
berbeda, maka kita tuliskan n(S) = 52. Di dalam satu set kartu bridge tadi terdapat 4 jenis
kartu yang berbeda.
- Kartu sekop (hitam) = 13 jenis
- Kartu hati (merah) = 13 jenis
- Kartu daun (hitam) = 13 jenis
- Kartu intan (merah) = 13 jenis
Dalam setiap jenis kartu, terdapat 3 kartu bergambar
a.l :
- Kartu Jack (J)
- Kartu King (K)
- Kartu Ratu (Q)
Sehingga kejadian mendapatkan kartu bergambar dapat kita misalkan A, dan kemungkinan munculnya n(A) = 12. Angka 12 kita peroleh
dari 3 kartu bergambar dalam 4 jenis kartu bridge ( 3 x 4 = 12). Maka peluang mendapatkan kartu bergambar P(A).
Soal : 11
Dari satu set kartu bridge, diambil satu kartu secara acak. Maka peluang mendapatkan kartu hati …
A. 1
B. ¼
C. 4
D. 1/14
E. Lewati
Kunci : B
Pembahasan
Satu set kartu bridge terdiri dari 52 kartu yang
berbeda, maka kita tuliskan n(S) = 52. Di dalam satu set kartu bridge tadi terdapat 4 jenis
kartu yang berbeda.
- Kartu sekop (hitam) = 13 jenis
- Kartu hati (merah) = 13 jenis
- Kartu daun (hitam) = 13 jenis
- Kartu intan (merah) = 13 jenis
Kemungkinan mendapatkan kartu hati ada 13, dan kita misalkan n(B) = 13. Sehingga kita dapat menghitung peluangnya.
Soal : 12
Dua buah dadu dilemparkan ke atas secara bersamaan. Maka peluang munculnya mata dadu berjumlah 10 adalah …
A. 1
B. ½
C. 2
D. 1/12
E. Lewati
Kunci : D
Pembahasan
Satu dadu {1,2,3,4,5,6} dan ada dua dadu dilemparkan
secara bersamaan. Maka sampelnya dapat kita tuliskan n(S) = 36, yang diperoleh
dari 6 x 6 = 36.
Kejadian dua dadu berjumlah 10 kita misalkan A, maka
kemungkinan yang terjadi A = {(4,6), (5,5), dan (6,4)}. Sehingga kejadian A
dapat kita tuliskan menjadi n(A) = 3.
Peluang :
Soal : 13
Dua buah dadu dilempar ke atas secara bersamaan. Maka
peluang munculnya mata dadu berjumlah sama.
A. 1
B. 1/6
C. 6
D. 1/16
E. Lewati
Kunci : B
Pembahasan
Satu dadu {1,2,3,4,5,6} dan ada dua dadu dilemparkan
secara bersamaan. Maka sampelnya dapat kita tuliskan n(S) = 36, yang diperoleh
dari 6 x 6 = 36.
Kita misalkan kejadian munculnya mata dadu berjumlah sama adalag A. Maka A = {(1,1), (2,2), (3,3), (4,4), (5,5) dan (6,6)} dan kita
tuliskan n(A) = 6.
Maka peluang A,
Soal : 14
Dua buah dadu dilemparkan ke atas secara bersamaan. Maka peluang munculnya mata dadu berjumlah 13 adalah …
A. 1
B. 0
C. 2
D. 4
E. Lewati
Kunci : B
Pembahasan
Satu dadu {1,2,3,4,5,6} dan ada dua dadu dilemparkan
secara bersamaan. Maka sampelnya dapat kita tuliskan n(S) = 36, yang diperoleh
dari 6 x 6 = 36.
Kejadian munculnya mata dadu berjumlah 13 kita misalkan sebagai A. Dan perlu dicatat, kejadian yang mungkin adalah jumlah mata
dadunya 12. Sehingga kita dapat menuliskan n(A) = 0.
Maka peluang A,
Soal : 15
Ada 10 ekor kuda sedang berlomba dalam pacuan kuda. Tiap – tiap kuda diberi nomor 1, 2, 3, 4, 5, 6, 7, 8, 9, dan 10. Maka peluang
kuda bernomor 3, 4, dan 7 berturut – turut keluar sebagai pemenang lomba.
Juara
1, juara 2, dan juara 3 dalam pacuan tersebut.
A. 1/12
B. 1/72
C. 1/120
D. 1/720
E. Lewati
Kunci : D
Pembahasan
Langkah pertama,
Kita carikan terlebih dahulu ruang sampelnya. Banyaknya cara agar 3 dari 10 ekor kuda keluar sebagai pemenangnya dengan
mempertimbangkan “urutan pemenang”. Maka untuk itu kita gunakan teori Permutasi,
Sekarang kita sudah dapatkan ruang sampel
n(S) = 720.
Langkah kedua (terakhir)
Kita menghitung peluang kuda bernomor 3, 4, dan 7 keluar sebagai pemenang lomba. Dengan satu kemungkinan juara 1, juara 2 dan juara
3.
Soal : 16
Dalam suatu kantong terdapat 5 bola merah dan 3 bola
biru. Kemudian diambil dua bola, bola pertama diambil dan tidak dikembalikan
lagi ke dalam kantong. Kemudian bola kedua diambil dan tidak dikembalikan.
Maka
peluang bola yang terambil berbeda warna adalah …
A. 30/112
B. 15/64
C. 15/56
D. 30/64
E. 30/56
Kunci : C
Pembahasan
Pengambilan bola 1, misalkan bola merah,
maka P(merah) = 5/8.
Pengambilan bola 2, misalkan bola biru,
maka P(biru) = 3/7.
Maka peluang terambilnya bola dengan beda warna,
Soal
: 17
Dari 10 peserta kontes kecantikan yang masuk nominasi, akan dipilih 3 nominasi terbaik secara acak. Maka banyak pilihan yang dilakukan
…
A. 10
B. 20
C. 40
D. 120
E. 720
Kunci
: D
Pembahasan
Dari soal diketahui ada 3 nominasi tanpa pengurutan, maka kita dapat menggunakan teori kombinasi ( C ).
Soal
: 18
Jika A adalah suatu kejadian dan P(A) merupakan peluang terjadinya A. Maka besarnya frekuensi harapan kejadian A dalam n kali
percobaan dapat dirumuskan…
Kunci : A
Pembahasan –
Soal : 19
Sekeping uang koin logam ditos sebanyak 30 kali. Maka frekuensi
harapan munculnya gambar adalah …
A. 5 kali
B. 10 kali
C. 15 kali
D. 20 kali
E. 25 kali
Kunci : C
Pembahasan
Pada pelemparan koin logam, peluang munculnya gambar
adalah ½ sebab P(A,G) = ½. Maka frekuensi munculnya gambar dalam 30 kali
pelemparan (tos).
Soal
: 20
Sebuah dadu dilemparkan ke atas sebanyak 60 kali. Maka
frekuensi harapan muncul angka ganjil …
A. 10 kali
B. 15 kali
C. 20 kali
D. 30 kali
E. 60 kali
Kunci
: D
Pembahasan
Mata dadu {1,2,3,4,5,6} dan mata dadu ganjil
A =
{1,3,5} maka peluang mata dadu ganjil.
Frekuensi harapan dadu ganjil,
Mengajar dalam Foto


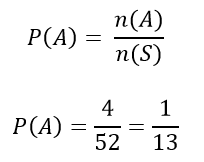







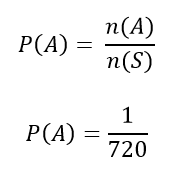










Tidak ada komentar:
Posting Komentar
Silahkan Berkomentar dengan Bijak sesuai dengan semangat kemajuan yang membangun Blog ini dan Jangan keluar dari topik