PERTEMUAN - 5 PERSAMAAN LINGKARAN
CONTOH SOAL
DAN PEMBAHASAN
Catatan
Persamaan
lingkaran yang berpusat di titik A(a,b)
dan melalui titik P(x1 , y1).
Dapat ditentukan dengan
menggunakan formula :
(
x – a )2 + ( y – b )2 = ( x1 – a )2
+ ( y1 – b )2
Dan
jari – jari,
r2
= ( x1 – a )2 + ( y1 – b )2
Contoh : 01
Tentukan
pusat dan jari – jari setiap lingkaran berikut
a)
(
x – 1 )2 + ( y – 2 )2 = 25
b)
(
x – 3 )2 + ( y + 1 )2 = 16
c)
(
x + 3 )2 + ( y – 2 )2 = 9
d)
(
x + 4 )2 + ( y + 5 )2 = 24
Pembahasan
Bentuk Umum : ( x – a )2 + ( y – b )2
= r2
Bagian a)
Dari sini dapat kita
simpulkan a = 1,
dan nilai b = 2.
Sedangkan nilai jari – jari r = 5.
Titik pusat
lingkaran, (1,2)
Jari – jari
lingkaran, r = 5
Kesimpulan :
Dengan cara yang sama
dapat kita lakukan
untuk b, c, dan d.
Bagian b)
(
x – 3 )2 + ( y + 1 )2 = 16
titik pusat
lingkaran ( 3, – 1)
jari – jari
lingkaran, r = 4 satuan
Bagian c)
(
x + 3 )2 + ( y – 2 )2 = 9
titik pusat lingkaran, (– 3, 2)
jari – jari lingkaran, r = 3 satuan
Bagian d)
(
x + 4 )2 + ( y + 5 )2 = 24
titik pusat
lingkaran, (– 4,– 5)
jari – jari
lingkaran, r = 2√6 satuan
Catatan
Pusat lingkaran merupakan titik tengah ruas
garis AB.Jika A(xA,yA) dan titik B(xB,yB).
Maka,
Contoh : 02
Tentukan persamaan
lingkaran yang diameter
merupakan garis yang menghubungkan titik
A(1,5) dan
B(9, – 1).
Pembahasan :
titik pusat lingkaran,
jari – jari
lingkaran,
Maka
persamaan lingkaran :
Contoh : 03
Tentukan
persamaan tempat kedudukan titik A
yang bergerak sehingga jaraknya terhadap
titik
O(0,0) senantiasa sama dengan 2 kali jaraknya
terhadap titik B(3,0).
Pembahasan
:
maka
persamaan lingkaran L ≡ (x – 4)2
+ y2 = 4
Catatan
:
Penentuan
persamaan lingkaran berpusat
di A(a,b) serta menyinggung garis Ax + By + C = 0,
lebih mudah jika menggunankan rumus
berikut.
Contoh :
Tentukan
persamaan lingkaran yang berpusat
di A(2,3) serta menyinggung garis berikut :
a)
Sumbu
x
b)
Sumbu
y
c)
8x
– 6y + 10 = 0
d)
2x
+ 3y + 4 = 0
e)
X
– 5 = 0
f)
Y
+ 2 = 0
Pembahasan :
Bagian a)
Pusat di A(2,3)
menyinggung sumbu x,
berarti bentuknya y = 0
Bagian b)
Pusat di A(2,3)
menyinggung sumbu y,
berarti bentuknya x = 0
Bagian c)
Pusat di A(2,3) menyinggung garis
8x – 6y + 10 = 0
ó
Ax + By + C = 0
ó
8x – 6y + 10 = 0
Bagian d)
Pusat di A(2,3)
menyinggung garis 2x + 3y + 4 = 0
Bagian e)
Pusat di A(2,3)
menyinggung garis x – 5 = 0
Bagian f )
Pusat di A(2,3)
menyinggung garis y + 2 = 0











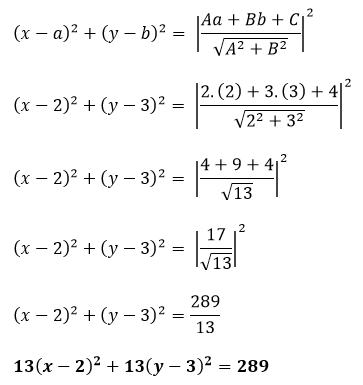





Komentar
Posting Komentar
Silahkan Berkomentar dengan Bijak sesuai dengan semangat kemajuan yang membangun Blog ini dan Jangan keluar dari topik