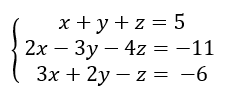SISTEM PERSAMAAN LINEAR TIGA VARIABEL

Daftar Isi :

1.     Defenisi Sistem Persamaan Linear Tiga Variabel

2.     Menyelesaikan Sistem Persamaan Linear Tiga Variabel

2.1   Metode Substitusi

2.2   Metode Eliminasi

      3.     Uji Kompetensi

 

1.         Sistem Persamaan Linear Tiga Variabel

 

Setiap persamaan yang berbentuk : ax + by + cz = d. Dengan a, b, c, dan d adalah konstanta. Dan a, b, dan c tidak sama dengan nol, maka persamaan tersebut dinamakan “Persamaan linear tiga variabel”. Himpunan titik – titik yang memenuhi persamaan tersebut, yaitu {(x,y,z) | ax + by + cz = d} adalah suatu bidang datar dalam sumbu – sumbu ortogonal x, y, dan z.

 

Bentuk umum sistem persamaan linear dengan tiga variabel :

 

        

Yang hanya mempunyai satu penyelesaian untuk x, y, dan z, yaitu {x,y,z}.

 

2.         Menyelesaikan Sistem Persamaan Linear Tiga Variabel

 

Untuk mencari penyelesaiannya, serupa dengan persamaan linear dua variabel, yaitu menggunakan metode Subsitusi dan Eliminasi.

 

2.1   Metode Substitusi

 

Penyelesaian sistem persamaan linear tiga variabel (dalam variabel – variabel x, y, dan z) dengan menggunakan metode substitusi ditentukan melalui langkah – langkah sebagai berikut.

 

i.            Pilihlah salah satu persamaan yang sederhana. 

        Nyatakan x sebagai fungsi y dan z, atau y sebagai 

        fungsi x dan z, atau z sebagai fungsi x dan y.

ii.          Substitusikan x, atau y, atau z yang diperoleh pada langkah 1 

        ke dua persamaan yang lainnya sehingga diperoleh sistem 

        persamaan linear dua variabel.

iii.        Selesaikan sistem persamaan linear dua variabel yang diperoleh 

        pada langkah 2.

iv.        Substitusikan dua nilai variabel yang diperoleh pada langkah 3

        ke salah satu persamaan semula untuk memperoleh nilai 

        variabel yang ketiga.

 

 

 

2.2   Metode Eliminasi

Penyelesaian sistem persamaan linear tiga variabel (dalam variabel – variabel x, y, dan z) dengan menggunakan metode eliminasi ditentukan melalui langkah – langkahnya  sebagai berikut :

i.    Eliminasi salah satu variabel, x atau y atau z sehingga diperoleh 

      sistem persamaan linear dua varibel.

ii.     Selesaikan sistem persamaan linear dua variabel pada langkah 1 

      sehingga diperoleh nilai dua variabel, x dan y atau x dan z atau y dan z.

iii.   Substitusikan nilai – nilai variabel yang diperoleh pada langkah 2 

      ke salah satu persamaan semula untuk mendapatkan nilai 

      variabel yang ketiga.

 

Contoh :

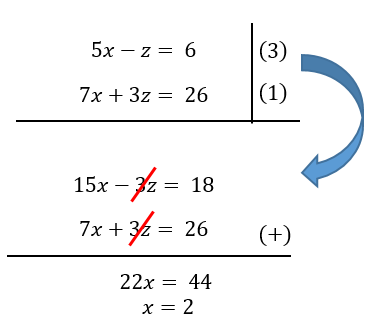
Selesaikan sistem persamaan linear di bawah ini dengan metode eliminasi.

 

 

Pembahasan :

Kita pilih persamaan (1) dan persamaan (2)

            

 

kemudian persamaan (2) dan persamaan (3) 

            

Persamaan (4) dan persamaan (5) merupakan persamaan linear dua variabel.

 

            

 

 

 

 

 

 

 

 

 

 

 

Setelah mendapatkan nilai x = 2, langkah berikutnya memasukan nilai x ke dalam persamaan (4) atau persamaan (5). Kita pilih persamaan (4) saja dan mensubstitusikan nilai x ke dalam persamaan (4).

 

 

Setelah kita peroleh nilai x dan z, yang tersisa adalah variabel y. Selanjutnya kita memilih persamaan (1) atau persamaan (2) atau persamaan (3), untuk mendapatkan nilai y. Kita memilih persamaan (1) saja.

Himpunan penyelesaian, HP = {2, 3, 4}

 

3.         Uji Kompetensi

 

Pilihlah satu jawaban yang benar

 

1.     Himpunan penyelesaian dari x + y + z = 4 ; 

     4x + 2y – 0,5z = – 1,5 ;  2x – 3y – 3z = – 17

A.   {– 3, 5, 2}

B.   {– 1, 2,– 3}

C.   {– 1, 2, 3}   

D.   {1, 8, – 5}

E.    {3, 2. – 1}

 

2.     Diketahui sistem persamaan x + y + 2z = 6 ; 

     x – y + z = – 4 ; 2x + y – 2z = – 4. Nilai xyz adalah …

A.   – 16

B.   – 4

C.   4

D.   8

E.    16

 

3.     Diketahui sistem persamaan :

 

            

 

Nilai x yang memenuhi adalah …

A.   4

B.   6

C.   8

D.   10

E.    12

 

4.   Nilai x + y + z , jika diketahui 2x + y – 3z = 3 ; 

    x – y + 5z = – 2 ; 2x + 2y – z = – 1 adalah …

A.   – 4

B.   – 3

C.   – 2

D.   – 1

E.    2

 

5.     Parabola y = ax² + bx + c melalui titik (1,0),(– 3, 16), 

      dan (2,1). Persamaan parabola tersebut adalah …

A.   y = x² – 2x + 1

B.   y = x² – 2x + 2

C.   y = x² + 2x – 1  

D.   y = x² + 2x – 3  

E.    y = x² + 3x – 4  

 

6.     Nilai x yang memenuhi sistem persamaan

 

 

adalah …

A.   – 3

B.   – 2

C.   – 1

D.   1

E.    3

7.     Himpunan penyelesaian sistem persamaan

 

 

adalah {(a, b, c)}. Nilai a x b x c = …

A.   36

B.   35

C.   30

D.   – 30

E.    – 36

 

8.     Sistem persamaan

 

 

Mempunyai penyelesaian x = 1, y = – 1, dan z = 2. 

Nilai a, b, dan c berturut – turut adalah …

A.   { 1, - 1, 2}

B.   { 3, 2, - 3}

C.   { - 3, 1, 4}

D.   { 4, - 1, - 1}

E.    { 2, - 1, 1}

 

9.     Diketahui sistem persamaan

 

 

Nilai x + 2y – 3z = …

A.   – 5

B.   – 3

C.   – 1

D.   3

E.    5

 

10.      SISTEM PERSAMAAN LINEAR TIGA VARIABEL

        A.   ( - 1, 5)

        B.   ( 2, 1)

        C.   ( 3, - 1)

        D.   ( - 3, 1)

        E.    ( 4, - 5 )      

 

Read More