SOAL :
Tentukan hasil bagi dan sisa dari pembagian suku banyak
P(x) = x4 – 3x2 + 2x – 1 oleh x2 – x – 2
dengan metode bagan Horner.
Pembahasan :
Sebelum kita bahas menggunakan bagan Horner,
saya mencoba membahasnya dengan menggunakan
metode bersusun.
Metode I :
Metode bersusun
Hasil Bagi, HB : x2 + x
Sisa, S(x) : 4x – 1
Untuk metode II merupakan teorema sisa dengan
menggunakan bagan Horner.
Metode II :
( x2 – x – 2 ) = ( x – 2 )( x + 1 )
ó x – 2 = 0
X = 2
ó x + 1 = 0
X = - 1
HB : x3 – x2 – 2x + 4
S(x) : - 5
Misalkan S(x) = ax + b
Bentuk Umum, BU : f(x) = g(x).H(x) + S(x)

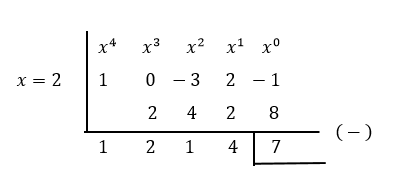
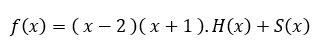







Tidak ada komentar:
Posting Komentar
Silahkan Berkomentar dengan Bijak sesuai dengan semangat kemajuan yang membangun Blog ini dan Jangan keluar dari topik