Daftar Isi :
Teori
1. Defenisi
Pusat di titik O(0,0) dengan r = √3
Bagian c)
Pusat di titik O(0,0) dengan r = 2 + √3
Bagian d)
Pusat di titik O(0,0) dengan r = 3 - √2
Pembahasan :
Bagian a)
Karena lingkaran x2 + y2 = r2 melalui titik A(2,4),
maka nilai r2 ditentukan
Bagian b)
Karena lingkaran x2 + y2 = r2 melalui titik E(a,2),
maka nilai r2 ditentukan
ó x2 + y2 = r2
ó a2 + 22 = r2
ó r2 = a2 + 4
ó maka pers. Lingkarannya menjadi
x2 + y2 – (a2 + 4) = 0
Contoh : 03
Tentukan tempat kedudukan titik – titik P(x,y) yang
memenuhi setiap hubungan berikut :
a) {P(x,y) / PB = 4 PA}, apabila A(0,1) dan B(0,16)
b) {P(x,y) / PB = 2 PA }, apabila A(1,0) dan B(4,0)
Pembahasan :
Bagian a)
Jadi, tempat kedudukan titik – titik P(x,y)
tersebut adalah lingkaran yang berpusat di
O(0,0) dan berjari – jari 4.
Bagian b)
ó PB = 2PA (ruas kiri dan kanan kita kuadratkan)
ó (PB)2 = 4(PA)2
ó (4 – x)2 + (0 – y)2 = 4[(1 – x)2 + (0
– y)2]
ó 16 – 8x + x2 + y2
= 4[ 1 – 2x + x2 + y2 ]
ó 16 – 8x + x2 + y2
= 4 – 8x + 4x2 + 4y2
ó 3x2 + 3y2
= 16 – 4
ó 3x2 + 3y2
= 12
ó x2 + y2 = 4 atau x2 + y2 –
4 = 0
Jadi tempat kedudukan titik P(x,y) tersebut adalah
lingkaran yang berpusat di O(0,0)
dan berjari – jari 2.
Contoh : 04
Tentukan persamaan lingkaran yang berdiameter
(garis tengah) ruas garis AB untuk setiap pasang
titik A dan titik B berikut :
a. A(1, – 2) dan B(– 1, 2)
b. A(a, b) dan B(– a, – b)
Pembahasan :
Bagian a)
Cara I
Catatan :
Untuk menentukan titik pusat lingkaran,
Untuk jari – jari
Maka jari – jari, r :
Persamaan lingkaran dengan pusat di tittik
O(0,0) dan berjari – jari r = √5.
Maka persamaan lingkarannya x2 + y2 = 5.
Cara II
ó ( x – 1 )( x + 1 ) + ( y + 2 )( y – 2 ) = 0
ó ( x2 – 1 ) + ( y2 – 4 ) = 0
ó x2 + y2 – 5 = 0
ó x2 + y2 = 5
BU : ( x – a )( x + a )
+ ( y – b )( y + b ) = 0
Bagian b)
Pusat lingkaran :
Jari – jari lingkaran :
Maka persamaan lingkaran, L :
Secara umum, persamaan lingkaran yang melalui
titik ujung diameter AB dengan A( xA , yA ) dan
B( xB , yB
) dapat dirumuskan sbb :
BU : ( x – a )( x + a )
+ ( y – b )( y + b ) = 0
Contoh : 05
Tentukan persamaan lingkaran yang berpusat
di O(0,0) serta menyinggung masing – masing
garis berikut ini.
a. 3x + 4y + 10 = 0
b. 12x – 5y – 39 = 0
c. x – 5 = 0
d. y + 5 = 0
e. y – 3 = 0
f. x = – 7
Pembahasan :
Catatan,
Bagian a)
Bagian b)
Persamaan garis, 12x
– 5y – 39 = 0
Bagian c)
Persamaan garis, x
– 5 = 0
Bagian d)
Persamaan garis, y
+ 5 = 0
Bagian e)
Persamaan garis, y
– 3 = 0
Bagian f )
Persamaan garis, x
= – 7







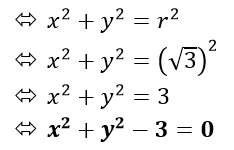








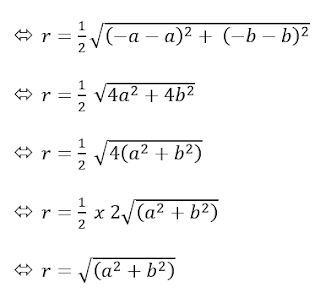








Tidak ada komentar:
Posting Komentar
Silahkan Berkomentar dengan Bijak sesuai dengan semangat kemajuan yang membangun Blog ini dan Jangan keluar dari topik