Garis – Garis pada Segitiga

BAB 6 Garis – Garis pada Segitiga

 

Daftar isi :

1.   Proyeksi

2.   Proyeksi Garis pada Segitiga

3.   Panjang Garis Tinggi pada Segitiga

4.   Dalil Steward

5.   Panjang Garis Berat pada Segitiga

6.   Garis Bagi

 

Selamat datang di blog saya,

Pada kesempatan kali ini, saya akan berbagi materi “Garis – Garis pada Segitiga”. Semoga pengalaman berbagi ini dapat memberikan manfaat buat kita semua, terima kasih.

 

1.   Proyeksi

Proyeksi adalah bayangan sinar datang dan bidang datar proyeksi selalu tegak lurus.

 

 

 

Berdasarkan gambar di atas :

Titik A’ adalah proyeksi titik A pada bidang datar dan AA’ tegak lurus pada bidang datar.

Titik B’ adalah proyeksi titik B pada bidang datar dan BB’ tegak lurus pada bidang datar.

Dengan demikian, A’B’ adalah proyeksi garis dari AB pada bidang datar.

 

2.   Proyeksi Garis pada Segitiga

  

 

Proyeksi garis AC pada sisi AB adalah AD, sedangkan BD adalah proyeksi dari garis BC pada sisi AB.

  

 

Rumus panjang proyeksi :

 

Catatan :

Sisi c adalah sisi proyeksi (tempat bayangan), sehingga panjang proyeksi dirumuskan sebagai : jumlah kuadrat sisi pengapit dari sudut yang ada pada sisi proyeksi dikurangi kuadrat sisi ketiganya ( di depan sudut tersebut), kemudian hasilnya dibagi dua kali panjang sisi proyeksi.

 

 

3.   Panjang Garis Tinggi pada Segitiga

 

Garis tinggi segitiga adalah garis yang tegak lurus sisi segitiga. Panjang garis – garis tinggi dalam sebuah segitiga berbanding terbalik dengan panjang sisi – sisi alasnya.

 

Pada ∆ABC berlaku :

 

 

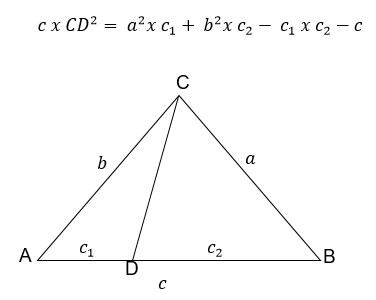
4.   Dalil Steward

Misalnya titik D pada sisi AB sehingga garis CD membagi AB menjadi c₁ : c₂.

Panjang CD dapat dihitung dengan menggunakan rumus :

 

 

5.   Panjang Garis Berat pada Segitiga

 

Garis berat adalah garis yang membagi dua sama panjang sisi di depannya. Jika CD adalah garis berat, maka c₁ : c₂ = ½ c. Berdasarkan dalil Steward, maka panjang garis berat ditentukan dengan rumus :

 

 

6.   Garis Bagi

Garis bagi adalah garis yang membagi sudut menjadi 2 bagian sama besar.